设备更新的决策,不仅是一个技术问题,也是一个经济问题。这正是设备综合管理的主要思想。下面介绍设备更新常用的两种经济评价方法。
1、经济寿命法
前面讲过,设备在使用过程中,设备的维修费用(或称使用费、运行费)会逐年增加,考虑到设备的初期投资,在开始阶段,设备的年均总费用会逐渐减少,到某一时刻,设备的年均总费用会达到最低,然后再逐年增高,见下图6-5。

图6-5 年均费用与使用年限的关系
k0,k1分别为设备购置费(初期投资)和设备最后的残值,G为第一年的运行费用,设备使用年数用T表示。为简单起见,假定每年的运行费用以λ递增,那么,平均每年分摊的费用(年均总费用C)就是: ![]()
根据上式求导,可以求出年均费用最低的设备使用年限,即经济寿命:
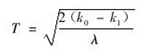
![]()
某设备初期购置费为 500 000 元,预计使用年限为 10 年。不考虑残值,第一年的运行费为 60 000 元,以后每年运行费等额递增 20 000 元。求设备的经济寿命。
运用上面的公式,可求出经济寿命为:
![]()
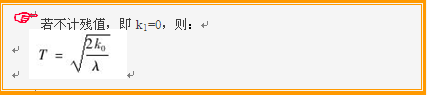
从上面的计算公式可以看出,设备的经济寿命与第一年的运行费用没有关系。而且,该公式的计算比较粗略,原因是:第一,每年的运行费用不可能是等额递增的,虽然递增的趋势是肯定的,但增加的速度不好确定;第二,设备的残值只考虑了预计使用年限的最终残值,在计算过程中,由于设备的经济寿命可能达不到预计使用年限,若在经济寿命终结时更新设备,残值肯定与预计的最终残值不同,比最终残值要大得多。所以考虑到这两个方面的因素,采用下面的面值法要准确得多。
2、面值法
面值法主要适用于以下几种情况:
第一,不需要知道设备的使用寿命是多少;
第二,在不同的时间有不同的折旧费;
第三,每年的使用费、运行费不要求等额递增,视实际情况而定;
第四,仍然不考虑资金的时间价值。
假设:M 代表设备原值;
Ln代表第 n 年的实际残值;
yt代表第 t年使用费(或维持费);
Pn代表平均年度总费用。
则:
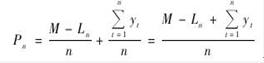
当 Pn<Pn-1且Pn<Pn+1时,n 即为设备的经济寿命周期。
![]()
假定设备的初期购置费为 18 000 元。各年的使用费及实际残值见下表:
表6-3各年的使用费及实际残值
| 使用年限(年) | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
残值(元) |
13,000 |
10,000 |
8,000 |
6,000 |
5,000 |
4,000 |
3,200 |
每年维修费(元) |
1,000 |
14,000 |
1,900 |
2,600 |
3,400 |
4,300 |
5,200 |
平均年度总费用P |
6,000 |
5,200 |
4,767 |
4,725 |
4,660 |
4,767 |
4,943 |
根据给出的条件,可分别计算出各年度的年均使用费:

以此类推,可得到其余年度的年均使用费,见表 6-3。从表中可见,平均年度总费用额从高到低,然后又从低到高,在第五年达到最低,说明设备的经济寿命应为 5 年。当然,在实际中,设备的经济寿命是否一定为 5 年,还要综合考虑其他方面的影响因素。